Backfitting algorithm
In statistics, the backfitting algorithm is a simple iterative procedure used to fit a generalized additive model. It was introduced in 1985 by Leo Breiman and Jerome Friedman along with generalized additive models. In most cases, the backfitting algorithm is equivalent to the Gauss–Seidel method algorithm for solving a certain linear system of equations
Contents |
Algorithm
Additive models are a class of non-parametric regression models of the form:
where each 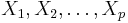 is a variable in our
is a variable in our  -dimensional predictor
-dimensional predictor  , and
, and  is our outcome variable.
is our outcome variable.  represents our inherent error, which is assumed to have mean zero. The
represents our inherent error, which is assumed to have mean zero. The 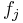 represent unspecified smooth functions of a single
represent unspecified smooth functions of a single 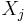 . Given the flexibility in the
. Given the flexibility in the 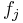 , we typically do not have a unique solution:
, we typically do not have a unique solution:  is left unidentifiable as one can add any constants to any of the
is left unidentifiable as one can add any constants to any of the 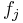 and subtract this value from
and subtract this value from  . It is common to rectify this by constraining
. It is common to rectify this by constraining
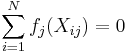 for all
for all 
leaving
necessarily.
The backfitting algorithm is then:
Initialize,
Do until
converge: For each predictor j: (a)
(backfitting step) (b)
(mean centering of estimated function)
where 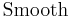 is our smoothing operator. This is typically chosen to be a cubic spline smoother but can be any other appropriate fitting operation, such as:
is our smoothing operator. This is typically chosen to be a cubic spline smoother but can be any other appropriate fitting operation, such as:
- local polynomial regression
- kernel smoothing methods
- more complex operators, such as surface smoothers for second and higher-order interactions
In theory, step (b) in the algorithm is not needed as the function estimates are constrained to sum to zero. However, due to numerical issues this might become a problem in practice.[1]
Motivation
If we consider the problem of minimizing the expected squared error:
There exists a unique solution by the theory of projections given by:
for i = 1, 2, ..., p.
This gives the matrix interpretation:
where 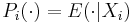 . In this context we can imagine a smoother matrix,
. In this context we can imagine a smoother matrix, 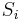 , which approximates our
, which approximates our 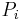 and gives an estimate,
and gives an estimate, 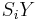 , of
, of 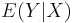
or in abbreviated form
An exact solution of this is infeasible to calculate for large np, so the iterative technique of backfitting is used. We take initial guesses 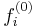 and update each
and update each 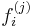 in turn to be the smoothed fit for the residuals of all the others:
in turn to be the smoothed fit for the residuals of all the others:
Looking at the abbreviated form it is easy to see the backfitting algorithm as equivalent to the Gauss–Seidel method for linear smoothing operators S.
Explicit derivation for two dimensions
For the two dimensional case, we can formulate the backfitting algorithm explicitly. We have:
If we denote 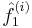 as the estimate of
as the estimate of 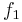 in the ith updating step, the backfitting steps are
in the ith updating step, the backfitting steps are
By induction we get
and
If we assume our constant  is zero and we set
is zero and we set 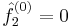 then we get
then we get
This converges if 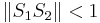 .
.
Issues
The choice of when to stop the algorithm is arbitrary and it is hard to know a priori how long reaching a specific conversion threshold will take. Also, the final model depends on the order in which the predictor variables 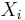 are fit.
are fit.
As well, the solution found by the backfitting procedure is non-unique. If  is a vector such that
is a vector such that 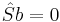 from above, then if
from above, then if 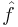 is a solution then so is
is a solution then so is 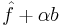 is also a solution for any
is also a solution for any 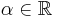 . A modification of the backfitting algorithm involving projections onto the eigenspace of S can remedy this problem.
. A modification of the backfitting algorithm involving projections onto the eigenspace of S can remedy this problem.
Modified algorithm
We can modify the backfitting algorithm to make it easier to provide a unique solution. Let 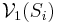 be the space spanned by all the eigenvectors of Si that correspond to eigenvalue 1. Then any b satisfying
be the space spanned by all the eigenvectors of Si that correspond to eigenvalue 1. Then any b satisfying 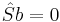 has
has 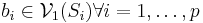 and
and 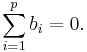 Now if we take
Now if we take  to be a matrix that projects orthogonally onto
to be a matrix that projects orthogonally onto  , we get the following modified backfitting algorithm:
, we get the following modified backfitting algorithm:
Initialize,
,
Do until
converge: Regress
onto the space
, setting
For each predictor j: Apply backfitting update to
using the smoothing operator
, yielding new estimates for
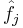
References
- ^ Hastie, Trevor, Robert Tibshirani and Jerome Friedman (2001). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer, ISBN 0-387-95284-5.
- Breiman, L. & Friedman, J. H. (1985). "Estimating optimal transformations for multiple regression and correlations (with discussion)". Journal of the American Statistical Association 80 (391): 580–619. doi:10.2307/2288473. JSTOR 2288473.
- Hastie, T. J. & Tibshirani, R. J. (1990). "Generalized Additive Models". Monographs on Statistics and Applied Probability 43.
- Härdle, Wolfgang et. al. (June 9, 2004). "Backfitting". http://fedc.wiwi.hu-berlin.de/xplore/ebooks/html/spm/spmhtmlnode37.html. Retrieved 2009-11-15.
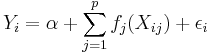
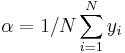
![\min E[Y - (\alpha %2B \sum_{j=1}^p \hat{f_j}(x_{ij}))]^2](/2012-wikipedia_en_all_nopic_01_2012/I/32bee1164f0a98aca67d6614a04a6a3e.png)
![f_i(X_i) = E[Y - (\alpha %2B \sum_{j \neq i}^p f_j(X_j)) | X_i)]^2](/2012-wikipedia_en_all_nopic_01_2012/I/1f0fae01c8db6ff312835e8a22673dca.png)
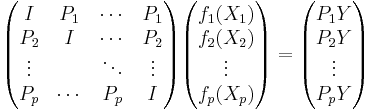
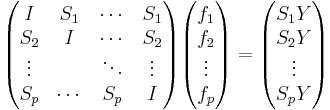
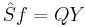
![\hat{f_i}^{(j)} \leftarrow \text{Smooth}[\lbrace y_i - \hat{\alpha} - \sum_{k \neq j} \hat{f_k}(x_{ik}) \rbrace_1^N ]](/2012-wikipedia_en_all_nopic_01_2012/I/f5753ae101668a71ca600d7b6a7074aa.png)
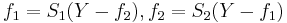
![\hat{f}_1^{(i)} = S_1[Y - \hat{f}_2^{(i-1)}], \hat{f}_2^{(i)} = S_2[Y - \hat{f}_1^{(i-1)}]](/2012-wikipedia_en_all_nopic_01_2012/I/34e40d860f4537078d1d858c0014a417.png)
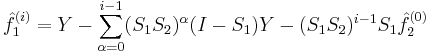
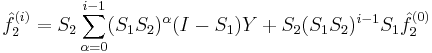
![\hat{f}_1^{(i)} = [I - \sum_{\alpha = 0}^{i-1}(S_1 S_2)^\alpha(I-S_1)]Y](/2012-wikipedia_en_all_nopic_01_2012/I/0b3b9e7194a9d3fc1243743981f201a7.png)
![\hat{f}_2^{(i)} = [S_2 \sum_{\alpha = 0}^{i-1}(S_1 S_2)^\alpha(I-S_1)]Y](/2012-wikipedia_en_all_nopic_01_2012/I/a3d08d212c2488e67912243bab8ff105.png)